tougenkyou

Solving simultaneous linear equations with matrices

math

tougen I'm having a few issues understanding reduced row echelon matrices in linear alg

Like how do you know a matrix has infinite solutions compared to 0 or 1 solutions? (edited)

And if the leading coefficient isn't 1 or 0, does it mean it's not a reduced row echelon right? Or do we need to use scaling too...idk if that would take too much time (edited)

Also why does the first diagonal row after the leading coefficient has to be 0s?

Do we use scaling (gaussian elimination) to solve this issue if they aren't 0 below the leading coefficient? (edited)

Tried my first augmented matrix idk if this is how you do it tho


ok let's take a step back n take a look at the case where there is 1 unique solution first i'm gonna do some examples in python with the sympy library, its basically like matlab and makes it ez to check ur work and try combinations of scaling swapping and adding/subtracting cuz ya its tedious af (edited)

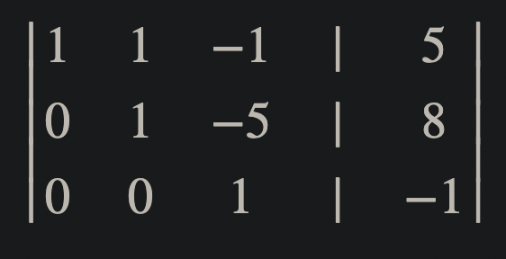
from sympy import Matrix, pprint

mat = Matrix([[1, 1, -1, 5], [0, 1, -5, 8], [0, 0, 1, -1]])
pprint(mat)

mat[0, :] = mat.row(0) - mat.row(1)
pprint(mat)

mat[0, :] = mat.row(0) - mat.row(2) * 4
pprint(mat)

mat[1, :] = mat.row(1) + mat.row(2) * 5
pprint(mat)
% kon_linalg_1_solution.py
(aug. matrix, the last column is the aug. part)
⎡1  1  -1  5 ⎤
⎢            ⎥
⎢0  1  -5  8 ⎥
⎢            ⎥
⎣0  0  1   -1⎦

⎡1  0  4   -3⎤
⎢            ⎥
⎢0  1  -5  8 ⎥
⎢            ⎥
⎣0  0  1   -1⎦

⎡1  0  0   1 ⎤
⎢            ⎥
⎢0  1  -5  8 ⎥
⎢            ⎥
⎣0  0  1   -1⎦
(to reduced row echelon form)
⎡1  0  0  1 ⎤
⎢           ⎥
⎢0  1  0  3 ⎥
⎢           ⎥
⎣0  0  1  -1⎦

so u know how the 1st column is x 2nd column is y 3rd is z, and the augmented is the x + y + z = SOMETHING column right
one unique solution is when the diagonal from top left to bottom right is all 1s in reduced row echelon form
and the rest are all zeroes
because then u get (or are tryna get)

1x + 0y + 0z = blah
0x + 1y + 0z = blah2
0x + 0y + 1z = blah3

Tried my first augmented matrix idk if this is how you do it tho

yes, you got it into row echelon form correctly! (edited)
here's another possible way

from sympy import Matrix, pprint

mat = Matrix([[2, 1, 0], [1, 2, 3], [-2, 2, 6]])
rref_form = mat.rref()
pprint(mat)
print()
# 1st row is index 0
mat[2,:] = mat.row(0) + mat.row(2)
pprint(mat)
print()

mat[1,:] = mat.row(0) - 2*mat.row(1)
pprint(mat)
print()

mat[1,:] = mat.row(1) + mat.row(2)
pprint(mat)
print()

# swap the 2nd & 3rd rows
mat[1,:],mat[2,:] = mat[2,:], mat[1,:]
pprint(mat)
print("the above matrix is now in in row ech form")
# diy reduction to red. row ech. form

mat[1,:] = mat.row(1) / 3
pprint(mat)
print()
mat[0,:] = mat.row(0) - mat.row(1)
pprint(mat)
print()
mat[0,:] = mat.row(0) / 2
pprint(mat)
print("the above matrix is now in red. row ech form")

print("compare to reduced by the computer:")
print(rref_form)



# matrix with only 1 solution
% python3 kon_linalg.py
⎡2   1  0⎤
⎢        ⎥
⎢1   2  3⎥
⎢        ⎥
⎣-2  2  6⎦

⎡2  1  0⎤
⎢       ⎥
⎢1  2  3⎥
⎢       ⎥
⎣0  3  6⎦

⎡2  1   0 ⎤
⎢         ⎥
⎢0  -3  -6⎥
⎢         ⎥
⎣0  3   6 ⎦

⎡2  1  0⎤
⎢       ⎥
⎢0  0  0⎥
⎢       ⎥
⎣0  3  6⎦

⎡2  1  0⎤
⎢       ⎥
⎢0  3  6⎥
⎢       ⎥
⎣0  0  0⎦
the above matrix is now in in row ech form
⎡2  1  0⎤
⎢       ⎥
⎢0  1  2⎥
⎢       ⎥
⎣0  0  0⎦

⎡2  0  -2⎤
⎢        ⎥
⎢0  1  2 ⎥
⎢        ⎥
⎣0  0  0 ⎦

⎡1  0  -1⎤
⎢        ⎥
⎢0  1  2 ⎥
⎢        ⎥
⎣0  0  0 ⎦
the above matrix is now in red. row ech form
compare to reduced by the computer:
(Matrix([
[1, 0, -1],
[0, 1,  2],
[0, 0,  0]]), (0, 1))

one stupid way to check whether something is in row ech form is if you can draw a staircase like this
you stop whenever you hit a non zero number (your leading coeff) (edited)
or the right edge
your staircase should only always go right, and never go left
0 solutions: so with this in mind, a matrix with no solutions (an unsolvable matrix), is if you ever run into a row where
0x + 0y + 0z + ... is NOT EQUAL to 0 (edited)

zero times x + zero times y, should always be zero, right, cuz basic math, 0 times anything is 0, if not, it's a contradiction (edited)
in practice, with row echelon form, you've already "made all the numbers as small as you can and tried to make a staircase with only 1s", so you only have to pay attention to the last row to see if you have all zeroes, and the aug. column is not zero

And if the leading coefficient isn't 1 or 0, does it mean it's not a reduced row echelon right?

1x + 0y + 0z = blah
0x + 1y + 0z = blah2
0x + 0y + 1z = blah3

however, if you do have a 1, then all the other numbers in that column must be zero , for this reason i outlined above

Like how do you know a matrix has infinite solutions compared to 0 or 1 solutions? i'll try to convey the intuition

if it has infinite solutions, it cannot have 0 solutions / be unsolvable. (edited)

0 solutions: so with this in mind, a matrix with no solutions (an unsolvable matrix), is if you ever run into a row where 0x + 0y + 0z + ... is NOT EQUAL to 0 (edited)

so you can rule this out first

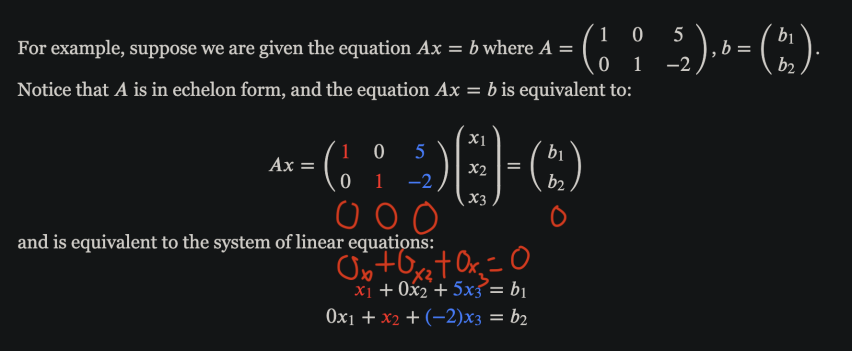
using this example, you have 3 variables, but only 2 equations.
so in effect, this means that you can set Z to any value, and still come up with a solution for X and Y (edited)
so the Z column here doesn't matter at all when trying to solve the system of eqs
geometrically, if you have 3 variables, you have a plane.
The intersection of 2 planes, is a line, with only 2 variables (Y = mX + b), and there r infinite points on a line (edited)
try karate chopping your hands together, so that they form an X

the middle of the X forms a line (edited)
the intersection of three planes is a point. like the corner of your room
in which case there would be a unique solution for x, y, and z
now that we have that out of the way, if you have a matrix where columns >= rows (not counting the aug. column) and you have a row that's all zeroes after reducing, you're gonna run into this situation, you have more variables than equations to solve for them

going back to your paper example after row reduction,

⎡1  0 | -1⎤
⎢     |   ⎥
⎢0  1 | 2 ⎥
⎢     |   ⎥
⎣0  0 | 0 ⎦

you might notice we have all zeroes
however, rows > columns (not counting aug)
if we take away that all-zeroed row, we still have enough information to get a unique solution for X and Y
Do we use scaling (gaussian elimination) to solve this issue if they aren't 0 below the leading coefficient?
gaussian elimination is just a super stupid way to repeatedly scale so that you get that "staircase leading coefficients" pattern (edited)
you're gonna get fractions if you do it, but it's fast (and what computers use!)
the idea is

you divide (or multiply if you have fractions...) until your leading coefficient is a 1
you zero-out everythnig above and below in your column, which is easy since you have 1, just scale and subtract (edited)
you can also do it the "intelligent" way like what you and i just did, but it's time consuming
cuz ur thinking of all the possibilities n how to make neat numbers i strongly recommend u go through this https://textbooks.math.gatech.edu/ila/row-reduction.html (some of the pictures 1 pasted r from here)
"pivot" is just another word for "leading coefficient" here
it will teach u how to spot which of the columns correspond to "free variables", which to simplify a bit are "redundant/contribute to the infinite solution problem", like how Z is redundant in my example